2 АЛГОРИТМІЧНІ (ІМІТАЦІЙНІ) МОДЕЛІ В ЕКОНОМІЦІ Й ПІДПРИЄМНИЦТВІ
2.1 Основні принципи алгоритмічного (імітаційного) моделювання з урахуванням невизначеності й конфліктності
Алгоритмічне (імітаційне) моделювання – це числовий метод дослідження систем і процесів за допомогою моделюючого алгоритму.
Щоразу, коли на хід процесу, що моделюється, впливає випадковий фактор, цей вплив імітується за допомогою спеціально організованого розіграшу (жеребкування). Таким способом будується випадкова реалізація явища, яке модулюється, що є одним з результатів дослідження. За результатами окремого досвіду, звичайно, не можна робити висновок щодо закономірностей досліджуваного процесу. Але при великій кількості реалізацій середні характеристики моделі (математичне очікування, мода, медіана) здобувають стійкі властивості, які підсилюються з ростом кількості реалізацій (прогонів). Звичайно, залишається певний ризик, який обумовлений неповнотою даних, невизначеністю тощо.
У складі трансляторів майже всіх алгоритмічних мов є стандартні процедури (функції), які генерують випадкові (точніше, псевдовипадкові) числа, які є реалізаціями послідовності випадкових чисел з рівномірним законом розподілу (генератори випадкових чисел).
Процес створення й машинної реалізації імітаційних моделей включає етапи:
- побудова концептуальної моделі;
- побудова алгоритму відповідно до концептуальної моделі системи;
- створення комп'ютерної програми;
- машинний експеримент із моделлю системи.
Є безліч прикладів систем, функціонування яких може бути досліджене за допомогою імітаційного моделювання. До таких систем відносять виробничі й торговельні підприємства, банки, біржі, енергосистеми, різні комунікаційні системи, бібліотеки, картотеки, склади і т.п.
Основна проблема моделювання подібних об'єктів міститься в особливій «конструкції» їхньої структури, відсутності достатньої кількості статистичних даних, неможливості проведення експерименту над реальними системами з метою збору необхідних даних і виявлення їхніх слабких сторін і відгуків на різні зовнішні впливи.
Ідея імітаційного моделювання базується на заміні експерименту над реальними об'єктами експериментом над їхніми моделями. У переважній більшості випадків саме відсутність статистичних даних не дозволяє виконати аналіз і прогноз реального процесу. Імітаційне моделювання надає можливість мати в розпорядженні аналоги таких даних, одержуючи їх не з життя, а з псевдореального функціонування моделі.
Одним з важливих аспектів у процесі роботи з імітаційною моделлю є аналіз її чутливості. Під ним розуміють визначення ступеня мінливості значень цільових показників моделі, обумовлених мінливістю (невизначеністю, варіабельністю) вихідних параметрів. Так, якщо при відносно невеликих змінах вихідних даних відбувається істотна зміна в результатах моделювання, то це є достатньою підставою для додаткових, більше детальних досліджень, зокрема, щодо взаємозв'язків між відповідними змінними.
Аналіз та узагальнення даних, накопичених у процесі імітаційних експериментів, досить часто дозволяє краще зрозуміти якісні й кількісні закономірності, властиві поведінці керованих об'єктів, і відобразити їх в аналітичному вигляді.
Імітаційні (алгоритмічні) моделі можуть бути детермінованими й стохастичними. В останньому випадку за допомогою генераторів випадкових чисел імітується вплив невизначених і випадкових факторів. Такий метод імітаційного моделювання отримав назву методу статистичного моделювання (або методу Монте-Карло). Метод Монте-Карло – це один з методів моделювання результатів функціонування складної системи, на яку впливають випадкові фактори і яка, як правило, не може бути описана ні якими іншими методами. Основний принцип, що лежить в основі методу Монте-Карло, полягає в наступному: реальні статистичні дані заміняють даними, отриманими на основі вибірки із чисел, які підкоряються тим самим законам розподілу, що й реальні дані.
Саме головне при цьому, що ці закони в моделях можна змінювати відповідно до можливих змін у реальних системах, які бажано змоделювати, не виконуючи такі експерименти над реальними системами.
На даний час цей метод вважають одним з найбільш ефективних методів дослідження складних систем, а часто і єдиним практично доступним методом одержання нової інформації щодо поводження гіпотетичної системи (на етапі її проєктування).
2.2 Використання законів розподілу випадкових величин при імітації економічних процесів
Для моделювання випадкової величини необхідно знати закон її розподілу. Для перетворення послідовності випадкових чисел, які являють собою реалізацію випадкової величини з рівномірним законом розподілу в інтервалі (0;1), у послідовність випадкових чисел, які є реалізаціями випадкової величини із заданою інтегральною функцією розподілу F(x), потрібно із сукупності випадкових величин з рівномірним законом розподілу в інтервалі (0;1) вибрати випадкове число й вирішити відносно х рівняння [4]:
У випадку, коли задана функція щільності розподілу f(x), співвідношення (2.1) приймає вид:
Для деяких законів розподілу отримано аналітичне рішення рівняння (2.2), результати якого наведені в таблиці 2.1
Таблиця 2.1 − Визначення щільності розподілу для деяких законів [4]

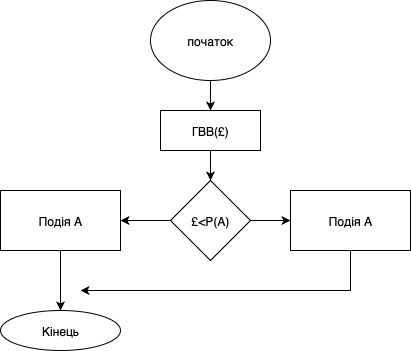
2.2.1 Моделювання простої події Нехай має місце подія А, імовірність настання якої дорівнює Р(А). Потрібно вибрати правило, у багаторазовому використанні якого частота появи події відповідала б її ймовірності. Виберемо за допомогою генератора випадкових чисел, що мають рівномірний закон розподілу на інтервалі (0;1), деяке число £, і визначимо ймовірність того, що £<Р(А). Для випадкового числа £, що є реалізацією випадкової величини з рівномірним законом розподілу на інтервалі (0;1), справедливою буде наступна залежність:
Отже, імовірність влучення випадкової величини в інтервал (0; Р(А)) дорівнює величині Р(А). Тому, якщо під час розіграшу число потрапило в цей інтервал, то варто вважати, що відбулася подія А. Протилежна подія (А) відбудеться з імовірністю (1−Р(А)) у тому випадку, коли £>=Р(А). Процедура моделювання простої події v в імітаційній моделі описується алгоритмом, схема якого представлена на рисунку 2.1 [4]. Через генератор випадкової величини ГВВ(£) на рисунку 2.1 позначено процедуру генерації випадкових величин £, які мають рівномірний закон розподілу на інтервалі (0; 1).
2.2.2 Моделювання випадкових величин з рівномірним законом розподілу Розглянемо важливий і дуже простий рівномірний розподіл випадкової величини на інтервалі (m−s, m+s). Щільність ймовірностей цього розподілу надається наступною формулою:
де m – математичне очікування; s – максимальне відхилення від математичного очікування. Такий розподіл використовується, коли про інтервали часу відомо лише те, що вони мають максимальний розкид, і нічого не відомо про розподіл ймовірностей цих інтервалів.
Генератор випадкових чисел [5] генерує послідовність реалізацій випадкової величини £ з рівномірною функцією розподілу на інтервалі (0;1). Якщо прийняти a=m−s і b=m+s, то для того, щоб одержати реалізацію випадкової величини з рівномірним розподілом на інтервалі (a,b), необхідно вирішити відносно х рівняння:
Рівномірний розподіл можна використовувати при розрахунках по сітьовим графікам робіт. Формула для визначення дисперсії має вигляд:
2.2.3 Моделювання випадкових величин з нормальним законом розподілу
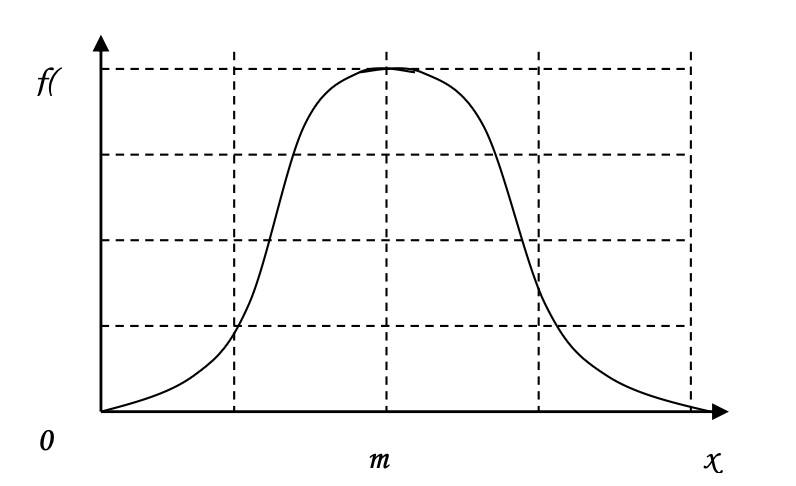
Нормальний, або гауссовий розподіл, – це, безсумнівно, одне з найбільш важливих і часто використовуваних видів безперервних розподілів. Воно симетрично щодо математичного очікування. Зупинимося на практичному змісті цього розподілу стосовно до економічних завдань і сформулюємо центральну граничну теорему теорії ймовірностей у наступній практичній інтерпретації.
Безперервна випадкова величина x має нормальний розподіл ймовірностей з параметрами m і σ>0, якщо її щільність ймовірностей розподілу має вигляд (рис. 2.2) [4]:
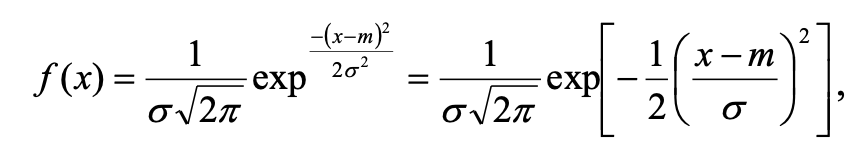 (2.7) є сумою n незалежних випадкових величин, які розподілені за невідомим законом і мають кінцевий третій абсолютний момент.
(2.7) є сумою n незалежних випадкових величин, які розподілені за невідомим законом і мають кінцевий третій абсолютний момент.
де m – математичне сподівання M[x]; σ – середньоквадратичне відхилення.
При цьому, якщо D[x] – це дисперсія, то середньоквадратичне відхилення .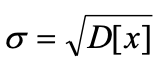 .
.
Приймемо, що випадкова величина
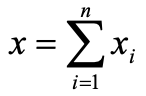 є сумою n незалежних випадкових величин, які розподілені за невідомим законом і мають кінцевий третій абсолютний момент.
є сумою n незалежних випадкових величин, які розподілені за невідомим законом і мають кінцевий третій абсолютний момент.
Рисунок 2.2 – Нормальний розподіл ймовірностей безперервної випадкової величини x
Тоді справедливою є теорема: якщо зробити граничний перехід і спрямувати т-->8 , то розподіл випадкової величини
x^2
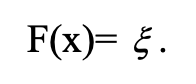
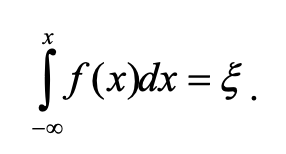
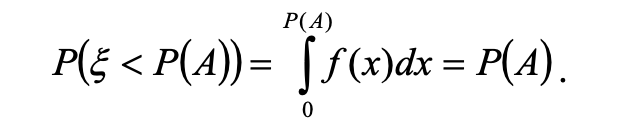
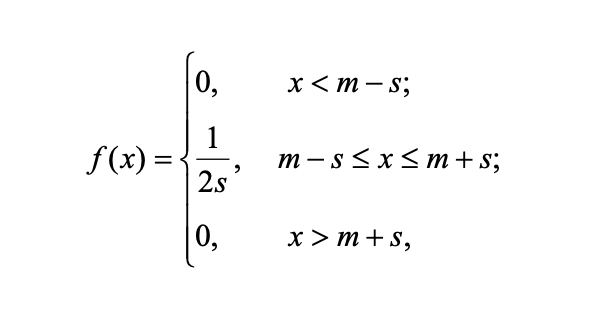
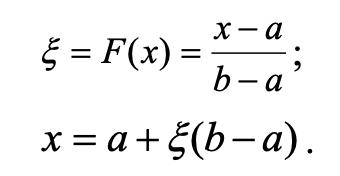
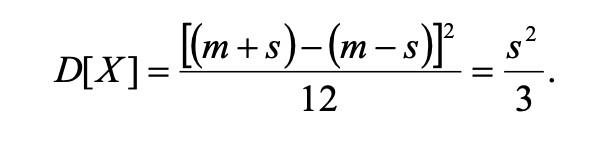
No comments to display
No comments to display