New Page

1.1 Економіка як об'єкт моделювання

Необхідно помітити, що поняття «економіка» має два значення: економіка може означати як науку, так і господарчу систему. Основне призначення економіки як господарчої системи – забезпечення суспільства предметами споживання і послугами, які створюють умови для життя й діяльності людини й суспільства в цілому. Економіка як економічна теорія – це суспільна наука, що вивчає аспекти прийняття рішень людьми з метою задовольнити наявні матеріальні потреби, використовуючи обмежені ресурси.

Центральним поняттям кібернетики є поняття «система». Системою називається комплекс взаємозалежних елементів разом з відносинами (зв'язками) між цими елементами і між їхніми атрибутами, які спільно реалізують визначені цілі. Основним методом дослідження систем є метод моделювання, тобто спосіб теоретичного аналізу і практичної дії, спрямований на розробку та використання моделей.

Модель – це уявний або реальний об'єкт, який у процесі вивчення заміщує об'єкт-оригінал.

Помітимо, що спектр різновидів моделей, які використовують економісти, досить широкий. Модель є інструментом економічного аналізу. І чим більш різноманітний інструментарій має у своєму арсеналі економіст, тим більшою є імовірність одержання достовірних результатів.

Об'єктом дослідження економіко-математичного моделювання являється економіка як соціально-економічна система.

Соціально-економічна система – це складна імовірнісна динамічна система, що охоплює процеси виробництва, обміну, розподілу і споживання матеріальних й інших благ [1]. Соціально-економічні системи належать до класу кібернетичних, тобто керованих, систем.

Одним з важливих аспектів в економіко-математичному моделюванні є поняття адекватності моделі, тобто відповідності моделі тому об'єкту або процесу, на підставі якого вона створюється. Адекватність моделі – трохи умовне поняття, оскільки повної відповідності моделі реальному об'єкту бути не може. Мова йде не просто про адекватність, а про відповідність тим властивостям, які є істотними для дослідника, відповідають меті дослідження і належній системі гіпотез. Відзначимо, що перевірка адекватності економіко- математичних моделей – дуже складний процес, обумовлений важкістю виміру економічних величин. Але без такої перевірки на адекватність використання результатів моделювання в аналізі й управлінських рішеннях може не тільки виявитися малокорисним, але й призвести до негативних наслідків.

Слід зазначити, що соціально-економічні системи належать до так званих складних систем, яким властивий ряд ознак, які потрібно враховувати під час моделювання. Інакше неможливо говорити про адекватність побудованої моделі. Серед цих ознак можна відзначити:

емерджентність, як прояв у самій яскравій формі властивості цілісності системи, тобто наявність в економічної системи таких особливостей, які не властиві жодному з її елементів, що розглядається окремо, поза системою;
динамічність економічних процесів, що полягає в зміні в часі параметрів і структури економічних систем під впливом як внутрішніх, так і зовнішніх факторів (навколишнього середовища);
невизначеність щодо розвитку економічних явищ (процесів);
неможливість ізолювати процеси, які здійснюються в економічних системах, від процесів у навколишньому середовищі, для того, щоб спостерігати і досліджувати їх незалежно;
активна реакція на нові фактори, що з'являються. Використовуючи системний підхід у дослідженні економіки, відрізняють зокрема, макро- і мікроекономічні моделі. Макроекономічні моделі відображають функціонування і розвиток всієї економічної системи або її великих підсистем. Мікроекономічні моделі відображають функціонування і розвиток господарських одиниць та їхніх об'єднань.

1.2 Моделювання як метод наукового пізнання

Модель – це образ реального об'єкта (процесу) у матеріальній або ідеальній формі, який відображає істотні властивості даного об'єкта (процесу) і заміщає його в ході дослідження при обраній системі гіпотез.

Математична модель – це «макет» реальності (миру), у якому взаємозв'язки між конкретними елементами, які цікавлять дослідника, замінені відносинами між математичними категоріями. Ці відношення, як правило, представлені у формі рівнянь, нерівностей, відносинами формальної логіки між показниками, які характеризують функціонування реальної системи, що моделюється.

Сутність методології математичного моделювання міститься в заміні досліджуваного об'єкта його «образом» – математичною моделлю – і наступним вивченням (дослідженням) моделі на підставі аналітичних методів і обчислювально-логічних алгоритмів, які реалізуються за допомогою комп'ютерних програм. Робота не із самим об'єктом (явищем, процесом), а з його моделлю дає можливість відносно швидко досліджувати його істотні властивості й поводження при будь-яких імовірних ситуаціях. У той же час комп'ютерні та імітаційні експерименти з моделями об'єктів, на відміну від сугубо теоретичних підходів, дозволяють досить ретельно і глибоко вивчати об'єкт.

При вивченні даної дисципліни основна увага приділяється моделям прийняття рішень: математичним моделям, у яких певні змінні представляють рішення, які потрібно (або принаймні можна) прийняти. Очевидно, що скоротити відстань між Києвом і Дніпром неможливо. Однак можна вибрати швидкість руху, кількість зупинок і час, витрачений на кожну з них. Це і є змінні рішення. На ці змінні також можна накладати певні обмеження – не можна їхати зі швидкістю більше 100 км/год, бензобак має обмежену ємність, заправлення вимагає певного часу й т.д. Подібні обмеження є основою побудови реалістичних моделей.

Схематично модель може бути представлена у вигляді «чорного ящика» (рис. 1.1).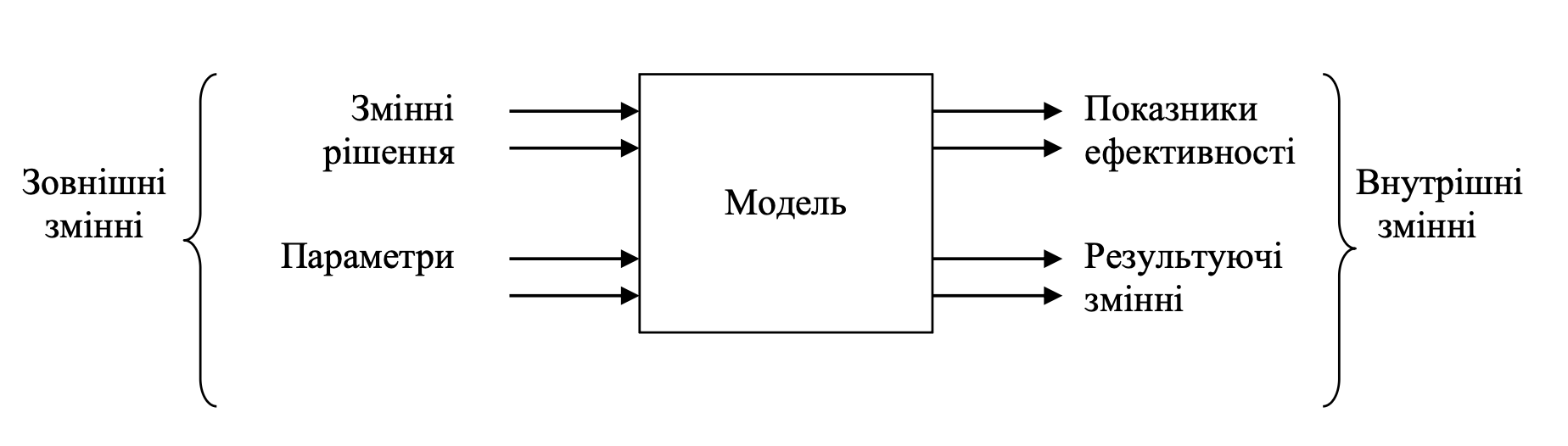Рисунок 1.1 – Модель у вигляді «чорного ящика»

У такому поданні деталі роботи моделі не розглядаються. Основна увага приділяється визначенню:

входів, тобто того, що модель повинна обробляти;
виходів – того, що модель робить. Модель на даному етапі називається «чорним ящиком», оскільки ще не відомо, яка логіка буде реалізована в моделі.

Після визначення входів і виходів моделі необхідно розбити їх на дві категорії. Входи, іменовані зовнішніми змінними, діляться на змінні рішення (тобто змінні, контрольовані менеджером) і параметри (тобто змінні, котрі менеджер контролювати не може).

Прикладами змінних рішення можуть служити сума, у яку менеджер оцінює свій продукт, розміщення виробничого устаткування або рішення, продавати філіал чи ні.

Прикладами параметрів можуть служити ціни, призначувані конкурентами на аналогічні товари або послуги, фізичні обмеження обсягу складського приміщення, вартість одиниці сировини або прогнозована кількість опадів. Багато неконтрольованих вхідних величин можуть бути невідомі заздалегідь. Трактуючи їх як параметри, можна будувати модель так, ніби вони були відомі. Пізніше можна конкретизувати чисельні значення даних величин, проаналізувавши дані й оцінивши ці значення, або просто задати передбачувані значення величин при аналізі моделі.

Виходи, іменовані внутрішніми змінними, діляться на показники ефективності (або критерії), які визначають ступінь наближення до мети, і результуючі змінні, які відображають інші наслідки моделювання і допомагають розуміти й інтерпретувати результати роботи моделі.

Критерії особливо важливі, тому що саме вони використовуються, щоб визначити, наскільки вдалося наблизитися до кінцевої мети. Тому критерії часто називають цільовими функціями.

Прикладами цільових функцій є дохід, частка ринку, сукупні витрати, дисципліна працівників, задоволення клієнта, доходи від інвестицій. Приклади результуючих змінних – розбивка доходу по статтях, кількість проданих виробів, сплачені податки й інші величини, які корисно знати.

Незважаючи на простоту концептуальної схеми «чорного ящика», вона змушує розроблювача на самому початку процесу моделювання визначити, що варто включити в модель, а що виключити з неї, а також розібратися із класифікацією відповідних факторів.

Розглянемо деякі запитання, на які може наштовхнути розроблювача моделі розглянута вище схема «чорного ящика»:

Що таке прибуток для даної приватної компанії – рішення або показник ефективності?
Якими повинні бути правильно сформовані множини змінних рішень на відміну від другорядних змінних? Наприклад, чи варто вважати ціну на свій продукт єдино важливим рішенням, припускаючи, що бюджет на рекламу зафіксований (кимсь іншим) на певному рівні, або потрібно розглядати і ціну продукту, і бюджет на рекламу як одночасно прийняті рішення?
Чи дійсно менеджер контролює ціну на свій продукт (у цьому випадку ціна є змінної рішення) або вона визначається конкуруючими силами ринку (у такому випадку ціна є параметром)?
Чи є кількість продукту, яку потрібно продати, змінною рішення, тобто контрольованим входом моделі, або кількість проданого продукту є виходом моделі (результуючою змінної), а входом є його ціна?
Чи є дисципліна працівників критерієм, тобто тим, на що менеджер може вплинути адміністративними способами, ухвалюючи рішення щодо людських ресурсів. Або це параметр, якому потрібно приймати як даність? У кожному разі, як виміряти дисциплінованість? Якщо це поняття занадто розпливчасто, щоб визначати його в якості змінної, може, варто не включати10 його в модель, а врахувати пізніше, на етапі інтерпретації моделі? Або варто використовувати як показник дисципліни кількість прогулів? Які фактори в такому випадку впливають на них, і яка підмножина цих факторів повинна стати змінними рішення?
Якщо частка ринку повинна бути критерієм, яке точне визначення ринку, на частку якого вплинуть рішення менеджера? Мається на увазі частка регіонального, національного або міжнародного ринку? Або всіх трьох? Чи йде мова про частку ринку цього року, у наступному році або в наступні п'ять років? У чому виміряється частка ринку – у кількості проданих одиниць товару або у вартісному вираженні?
Чи потрібно включати в модель продажу конкурентів як параметри? Адже якщо вважати продажу конкурентів зовнішніми входами, це означає, що менеджер не може впливати на них і повинен сприймати їх як задані. Однак менеджер, безумовно, може вплинути на обсяги продажів конкурентів за допомогою активної системи знижок або посиленої реклами, які можуть служити змінними рішення. У такому випадку приналежним конкурентам частка ринку повинна бути внутрішнім виходом (результуючою змінною), а не зовнішнім входом моделі. Але якщо це вихід моделі, може варто вважати частку ринку, що належить конкурентам, критерієм, який потрібно мінімізувати?
Менеджер повинен керуватися у своїй моделі лише своїми власними критеріями, тимчасовою шкалою і світоглядом або зобов'язаний ураховувати переваги свого керівництва?
Основна увага в моделі повинна приділятися щоденним оперативним рішенням, більш довгостроковому стратегічному плануванню або і тому і іншому? ому?
Що потрібно включити в модель у вигляді показників ефективності або параметрів, які виходять від зовнішніх зацікавлених осіб, таких як законодавці, групи споживачів і акціонери? Досліджувані нами надалі методи моделювання можна застосовувати незалежно від того, як визначені входи й виходи моделі. Однак наведені вище запитання ілюструють важливість суджень розроблювача для чіткого визначення елементів «чорного ящика».

1.3 Поняття «економіко-математичного» моделювання. Етапи моделювання

Якщо мова йде про математичну модель, що описує механізм функціонування певної гіпотетичної економічної або соціально-економічної системи, то таку модель називають економіко-математичною або просто економічною.

Під економіко-математичною моделлю розуміють концентроване вираження самих істотних економічних взаємозв'язків досліджуваних об'єктів (процесів) у вигляді математичних функцій, нерівностей і рівнянь.

У різних галузях знань, зокрема в економіці, етапи моделювання здобувають специфічні риси. Проаналізуємо послідовність і значимість етапів одного циклу економіко-математичного моделювання [2].

Етап 1. Постановка економічної проблеми і розробка концептуальної моделі. Головне на цьому етапі – чітко сформулювати сутність проблеми (мети дослідження), припущення, які приймаються, і ті запитання, на які необхідно одержати відповіді. З урахуванням мети дослідження проводиться якісний аналіз об'єкта, що моделюється; виділяються його найважливіші риси і властивості. З позиції системного підходу вивчається структура об'єкта і головні взаємозв'язки між його елементами (підсистемами). Обираються та обґрунтовуються основні показники і система гіпотез, які пояснюють поводження й розвиток об'єкта і на основі яких буде виконуватися наступна формалізація.

На цьому етапі моделювання широко застосовуються якісні методи опису систем, знакові і язикові моделі. Таке первісне наближене зображення системи називають концептуальною моделлю.

Етап 2. Розробка математичних моделей. Це етап формалізації економічної проблеми, вираження її у вигляді конкретних математичних залежностей і відносин (функцій, рівнянь, нерівностей тощо). На цьому етапі проводиться теоретичне (аналітичне) дослідження моделі, обираються методи дослідження і рішення. Метою теоретичного (аналітичного) дослідження є з'ясування загальних властивостей моделі. Найважливіший момент – доказ існування рішення для моделі.

Етап 3. Реалізація моделі у вигляді пакета прикладних програм (ППП) і проведення розрахунків. Цей етап включає розробку алгоритмів для числового рішення завдання, складання програм на ЕОМ (можливе використання існуючих ППП із відповідною адаптацією) і безпосереднє проведення розрахунків. Труднощі цього етапу визначені, насамперед, великою розмірністю економічних завдань і необхідністю обробки значних масивів інформації. Виконання числових «модельних» експериментів дозволяє вивчати «поводження» моделі при різних значеннях деяких умов. Дослідження, які проводяться за допомогою числових методів, можуть стати істотним доповненням до результатів аналітичного дослідження.

Етап 4. Перевірка адекватності моделі. Вимога адекватності суперечить вимогам простоти, і це варто враховувати, перевіряючи модель на адекватність. Початковий варіант моделі попередньо перевіряється відповідно до таких основних аспектів:

чи всі істотні параметри включені в модель;
чи містить модель несуттєві параметри;
чи правильно відображені функціональні зв'язки між параметрами;
чи правильно визначені певні обмеження на значення параметрів тощо.

Для встановлення ступеня відповідності створюваної моделі оригіналу використають такі методи:

порівняння результатів моделювання з окремими експериментальними результатами, отриманими в подібних умовах;
використання інших схожих моделей;
порівняння структури і функціонування моделі з прототипом.

Головним напрямком перевірки адекватності моделі досліджуваного об'єкта виступає практика. Але вона має потребу в нагромадженні статистики, що не завжди буває достатньої для одержання надійних даних.

Етап 5. Аналіз числових результатів і прийняття відповідних рішень. На цьому етапі результати досліджень надаються у вигляді, зручному для розгляду, і на основі їх обробки проводиться аналіз матеріалів дослідження моделі. На цьому, завершальному етапі виникає питання про правильність і повноту результатів моделювання, про можливості їх практичного використання, а також про ступінь досягнення цілей дослідження.

Аналіз результатів моделювання складається з оцінки точності результатів моделювання, оцінки стійкості результатів моделювання та оцінки чутливості результатів моделювання. Формування висновків та пропозицій є завершальним етапом моделювання, на якому підводяться підсумки та висловлюються думки щодо напрямків подальшого дослідження об’єкта моделювання [3].

Існують зворотні зв'язки між етапами, які виникають у результаті того, що в процесі дослідження можуть бути виявлені недоліки попередніх етапів моделювання. Те, що не вдається виправити на перехідних етапах моделювання, усувають в наступних циклах. Але результати кожного циклу мають і цілком самостійне значення. Почавши дослідження від побудови простої моделі, можна швидко одержати корисні результати, а потім перейти до створення більш удосконаленої моделі.

1.4 Класифікація економіко-математичних методів і моделей

Сутність економіко-математичного моделювання міститься в описі соціально-економічних систем і процесів у вигляді економіко-математичних моделей. Економіко-математичні методи варто розуміти як інструмент, а економіко-математичні моделі – як продукт процесу економіко-математичного моделювання.

Розглянемо питання класифікації економіко-математичних методів. Ці методи являють собою комплекс економіко-математичних дисциплін, що є сплавом економіки, математики й кібернетики. В складі економіко-математичних методів можна виділити наступні розділи:

економічна кібернетика: системний аналіз економіки, теорія економічної інформації й теорія керуючих систем;
математична статистика: економічні додатки даної дисципліни – вибірковий метод, дисперсійний аналіз, кореляційний аналіз, регресійний аналіз, багатомірний статистичний аналіз, факторний аналіз, теорія індексів й ін.;
математична економія і економетрія: теорія економічного росту, теорія виробничих функцій, міжгалузеві баланси, національні рахунки, аналіз попиту й споживання, регіональний і просторовий аналіз, глобальне моделювання й ін.;
методи прийняття оптимальних рішень, у тому числі дослідження операцій в економіці: оптимальне (математичне) програмування, у тому числі методи гілок і границь, мережні методи планування й управління, програмно-цільові методи планування й управління, теорія і методи управління запасами, теорія масового обслуговування, теорія ігор, теорія й методи прийняття рішень, теорія розкладів;
методи й дисципліни, специфічні окремо як для централізовано планованої економіки, так і для ринкової (конкурентної) економіки. До першого можна віднести теорію оптимального функціонування економіки, оптимальне планування, теорію оптимального ціноутворення, моделі матеріально-технічного постачання й ін. До других – методи, що дозволяють розробити моделі вільної конкуренції, моделі капіталістичного циклу, моделі монополії, моделі індикативного планування, моделі теорії фірми й т.д. Багато з методів, розроблених для централізовано планованої економіки, можуть виявитися корисними і при математичному моделюванні в умовах ринкової економіки;
методи експериментального вивчення економічних явищ: математичні методи аналізу й планування економічних експериментів, методи машинної імітації (імітаційне моделювання), ділові ігри, методи експертних оцінок, розроблені для оцінки явищ, що не піддаються безпосередньому виміру.

Перейдемо до питань класифікації економіко-математичних моделей. Єдиної системи класифікації таких моделей у цей час не існує, однак звичайно виділяють більше десяти основних ознак їхньої класифікації.

По загальному цільовому призначенню економіко-математичні моделі діляться на теоретико-аналітичні, використовувані при вивченні загальних властивостей і закономірностей економічних процесів, і прикладні, застосовувані в рішенні конкретних економічних завдань аналізу, прогнозування й керування.

Відповідно до загальної класифікації математичних моделей вони діляться на функціональні (модель поводження споживачів в умовах товарно-грошових відносин), структурні (модель міжгалузевих зв'язків) і структурно-функціональні.

За ступенем агрегування об'єктів моделювання моделі розділяються на макроекономічні (моделі, що відображають функціонування економіки як єдиного цілого) й мікроекономічні (моделі зв'язані з такими ланками економіки, як підприємства й фірми).
За метою створення і застосування виділяють балансові моделі, що виражають вимогу відповідності наявності ресурсів та їхнього використання; трендові моделі, у яких розвиток економічної системи, що моделюється, відображається через тренд (тривалу тенденцію) її основних показників; оптимізаційні моделі, що призначені для вибору найкращого варіанта з певного числа варіантів виробництва, розподілу або споживання; імітаційні моделі, які використовуються в процесі машинної імітації досліджуваних систем або процесів й інші.
По типу інформації, яка використовується в моделі, економіко- математичні моделі розділяються на аналітичні (побудовані на апріорній інформації) та ідентифіковані (побудовані на апостеріорній інформації).
За фактором часу моделі підрозділяються на статичні (всі залежності віднесені до одного моменту часу) і динамічні (описують економічні системи в розвитку).
За фактором невизначеності моделі діляться на жорстко детерміновані (результати на виході однозначно визначаються керуючими впливами) і стохастичні (імовірнісні) (на виході спостерігаються різні результати залежно від дії випадкового фактору).
За характеристикою математичних об'єктів економіко-математичні моделі можуть класифікуватися як матричні моделі, моделі лінійного й нелінійного програмування, кореляційно-регресійні моделі, моделі теорії масового обслуговування, моделі сіткового планування й керування, моделі теорії ігор та ін.
За підходом до досліджуваних соціально-економічних систем виділяють дескриптивні й нормативні моделі. При дескриптивному підході виходять моделі, призначені для опису й пояснення фактично спостережуваних явищ або для прогнозу цих явищ; як приклад дескриптивних моделей можна привести названі раніше балансові й трендові моделі, виробничі функції й функції купівельного попиту, створені на основі обробки статистичних даних.

При нормативному підході досліджують не те, яким чином організована й розвивається економічна система, а як вона повинна бути організована і як повинна діяти в контексті певних критеріїв. Прикладом можуть служити всі оптимізаційні моделі і нормативні моделі рівня життя.

По співвідношенню екзогенних та ендогенних змінних моделі розділяються на відкриті й закриті. Повністю відкритих моделей не існує;

модель повинна містити хоча б одну ендогенну змінну. Повністю закриті економіко-математичні моделі (тобто такі, які не містять екзогенних змінних), надзвичайно рідкі. Переважна більшість економіко-математичних моделей займає посередню позицію й розрізняється по ступені відкритості (закритості).

Запитання для самоконтролю і перевірки знань

Дати визначення соціально-економічної системи.
Назвати основні властивості соціально-економічних систем.
Визначити сутність поняття «модель».
Охарактеризувати сутність методології математичного моделювання.
Поняття економіко-математичної моделі.
Охарактеризувати основні етапи економіко-математичного моделювання.
Особливості перевірки адекватності економіко-математичних моделей.
Визначити класи математичних методів.

Тести

1.1. Моделі за обліком фактора часу підрозділяються на:

детерміновані й стохастичні;
аналітичні й ідентифіковані;
статичні й динамічні;
дескриптивні й нормативні.

1.2. Стохастичною моделлю є

модель, на виході якої спостерігаються різні результати залежно від дії випадкового фактору;
модель, у якій всі необхідні дані для моделювання точно відомі;
неповна математична модель;
математична модель, у якій існують змінні рішення й хоча б один показник ефективності.

1.3. До входів моделі (до зовнішніх змінних) можна віднести:

результуючі змінні;
змінні рішення та параметри;
критерії;

1.4. Економіко-математична модель:

змушує менеджера явно вказати поставлені цілі;
змушує менеджера явно вказати типи рішень, що впливають на цілі;
змушує менеджера чітко вказати обмеження, що накладаються на значення, які можуть приймати змінні;
має всі перераховані вище якості.

1.5. До детермінованих моделей відносять:

моделі лінійного й нелінійного програмування;
балансові моделі;
трендові моделі;
імітаційні моделі.

1.6. Змінні рішення економіко-математичної моделі, являють собою:

неконтрольовані змінні;
змінні, які визначають ступінь наближення до мети;
контрольовані змінні;
змінні, які допомагають розуміти та інтерпретувати результати роботи моделі.